What is Conic Section?- Definition, Overview, and Types

What is the Conic section?

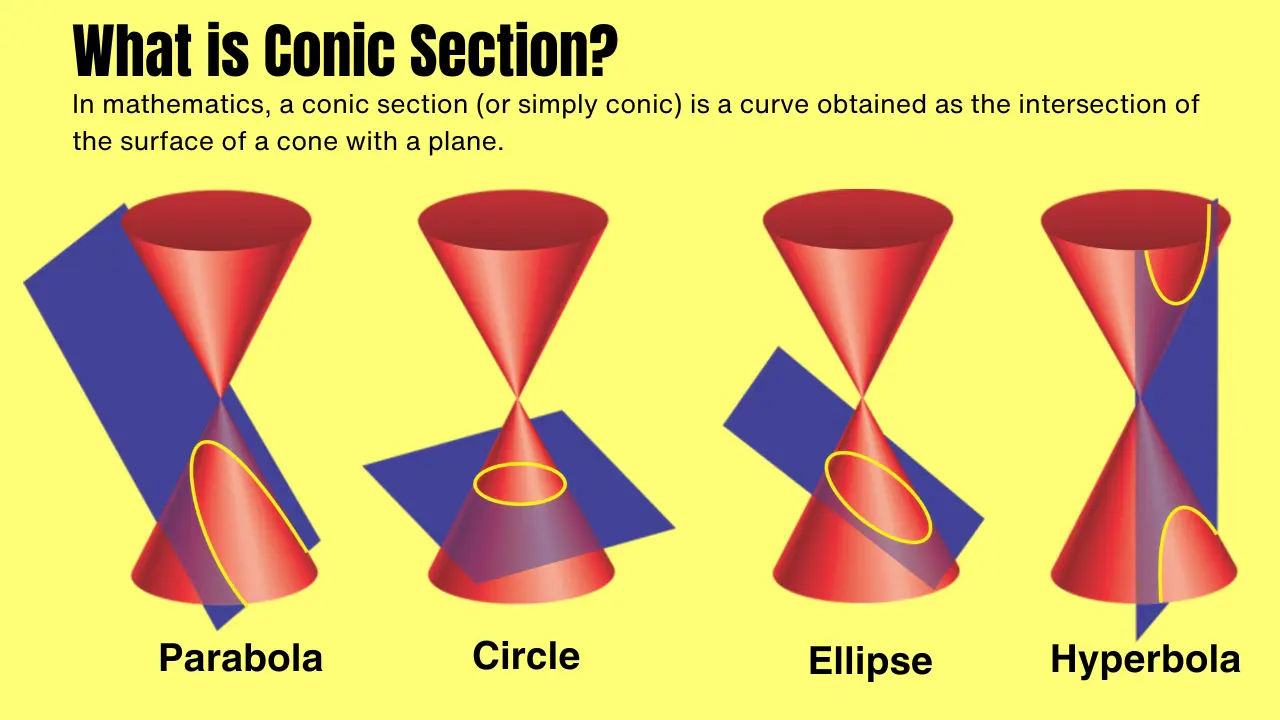
In mathematics, a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane.

The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type.

The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga’s systematic work on their properties.

The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions.

One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a focus, and some particular line, called a directrix, are in a fixed ratio, called the eccentricity.

The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2; that is, as the set of points whose coordinates satisfy a quadratic equation in two variables, which may be written in matrix form.

This equation allows deducing and expressing algebraically the geometric properties of conic sections. In the Euclidean plane, the three types of conic sections appear quite different but share many properties.

By extending the Euclidean plane to include a line at infinity, obtaining a projective plane, the apparent difference vanishes: the branches of a hyperbola meet in two points at infinity, making it a single closed curve; and the two ends of a parabola meet to make it a closed curve tangent to the line at infinity.

A further extension, by expanding the real coordinates to admit complex coordinates, provides the means to see this unification algebraically.

Key Takeaway:

• Ellipse is the locus of a point P which moves such that the ratio of its distance from the fixed-point F to its distance from a fixed line is a constant and is always less than 1.
• Parabola is the locus of a point Q which moves such that the ratio of its distance from the fixed-point F to its distance from the fixed-line is a constant and is always equal to 1.
• Hyperbola is the locus of a point R which moves such that the ratio of its distance from the fixed-point F to its distance from the fixed-line is a constant and is always greater than 1.

Definition

A conic is a curve obtained as the intersection of a plane, called the cutting plane, with the surface of a double cone (a cone with two nappes).

It is usually assumed that the cone is a right circular cone for the purpose of easy description, but this is not required; any double cone with some circular cross-section will suffice.

Planes that pass through the vertex of the cone will intersect the cone in a point, a line, or a pair of intersecting lines.

These are called degenerate conics and some authors do not consider them to be conics at all. Unless otherwise stated, “conic” in this article will refer to a non-degenerate conic.

There are three types of conics: the ellipse, parabola, and hyperbola. The circle is a special kind of ellipse, although historically Apollonius is considered as a fourth type.

Ellipses arise when the intersection of the cone and plane is a closed curve.

The circle is obtained when the cutting plane is parallel to the plane of the generating circle of the cone; for a right cone, this means the cutting plane is perpendicular to the axis.

If the cutting plane is parallel to exactly one generating line of the cone, then the conic is unbounded and is called a parabola.

In the remaining case, the figure is a hyperbola: the plane intersects both halves of the cone, producing two separate unbounded curves.

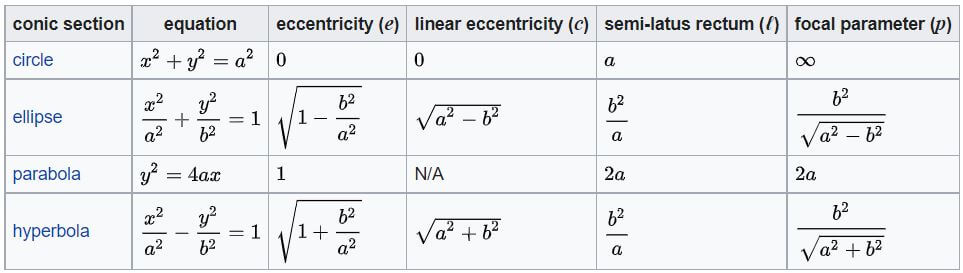
Equation, Eccentricity, Latus Rectum, Focal Parameter

Applications

Conic sections are important in astronomy: the orbits of two massive objects that interact according to Newton’s law of universal gravitation are conic sections if their common center of mass is considered to be at rest.

If they are bound together, they will both trace out ellipses; if they are moving apart, they will both follow parabolas or hyperbolas.

The reflective properties of the conic sections are used in the design of searchlights, radio telescopes, and some optical telescopes.

A searchlight uses a parabolic mirror as the reflector, with a bulb at the focus; and a similar construction is used for a parabolic microphone.

The 4.2-meter Herschel optical telescope on La Palma, in the Canary Islands, uses a primary parabolic mirror to reflect light towards a secondary hyperbolic mirror, which reflects it again to a focus behind the first mirror.

FAQs